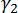Coefficient of Kurtosis

Kurtosis is a measure of how sharp the data peak is. Traditionally the value of this coefficient is compared to a value of 0.0, which is the coefficient of kurtosis for a normal distribution (i.e. the bell-shaped curve). A value greater than 0 indicates a peaked distribution and a value less than 0 indicates a flat distribution. Without a very large sample size, the use of this coefficient is of questionable value.

Population Kurtosis ( )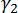

$image\popkurt.png$

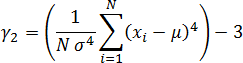
Sample Kurtosis ( )

$image\samkurt.png$

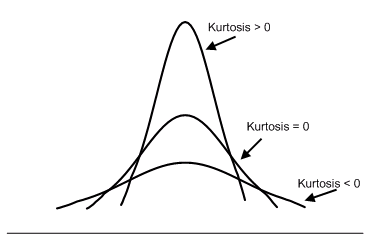
(adapted from King and Julstrom, 1982)

where

	= Population Standard Deviation
s	= Sample Standard Deviation
	= Population Mean
	= Sample Mean
N	= number of data values for a population
n	= number of data values for a sample
xi	= ith data value