The Anisotropy property of the Inverse distance gridding method lets you specify that data points in one direction from the lattice node have a higher weight than points in another direction. Points closer to the grid node are usually given more weight than points farther from the grid node, regardless of direction. If the points in one direction have more similarity than points in another direction, it is advantageous to give points in a specific direction more weight in determining the value of a lattice node. The relative weighting is defined by the anisotropy lengths of the three axes of the search ellipse or ellipsoid.
The available options for the Anisotropy setting are Isotropic, Anisotropic, and General. Isotropic sets all directions to equal weighting. Anisotropic allows an Ellipse to be specified to set the direction of weighting. The ellipse is along the X, Y, and Z axis directions. General allows each axis of the 3D ellipse to be manually altered. To change the Anisotropy setting, click on the existing option and select the desired option.
Natural phenomena are created by physical processes that often have preferred orientations. For example, course material settles out fastest at the mouth of a river while finer materials take longer to settle. Thus, the closer one is to the shoreline, the coarser are the sediments; the farther one is from the shoreline, the finer are the sediments. When interpolating a point, an observation 100 meters away but in a direction parallel to the shoreline is more likely to be similar to the value at the interpolation point than is an equidistant observation in a direction perpendicular to the shoreline. Anisotropy takes these trends in the data into account during the gridding process.
Anisotropy is useful when data sets use fundamentally different units in the X, Y, and Z directions. For example, consider plotting a flood profile along a river. The X coordinates are locations measured in miles along the river channel; the Y coordinates are measured in days; the Z coordinates are river depth; and the data values are water temperature, salinity, and concentration of pollutant. The X, Y, and Z coordinates are different units and most likely span different ranges, and one unit of X is not equal to one unit of Y or Z. Apply anisotropy to compensate for these differences.
Another example of anisotropy is creating an isotherm map of temperatures in the U.S. Although X and Y coordinates are in the same units, the Z or height units are different. In addition, temperatures tend to be most similar at constant Y and Z values, with more rapid variations as elevation and distance north of the equator change. When interpolating a lattice node, observations that lie in an east-west direction are given greater weight than observations lying an equivalent distance in the north-south direction or along the Z axis.
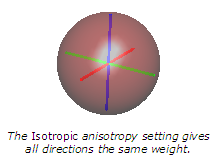
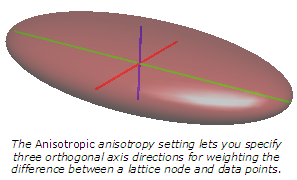
The Anisotropy property has three possible settings: Isotropic, Anisotropic, and General.
The Isotropic setting specifies that all directions are treated the same when weighting the distance between the lattice node and data point.

The Anisotropic setting lets you specify the lengths of the ellipsoid with orthogonal directions parallel to the X, Y, and Z axes. Points in the direction of the longest axis are given the most weight; points in the direction of the shortest axis are given the least weight. Voxler uses the anisotropy term Ellipse to refer to the three-dimensional ellipsoid. For example, if you specify the X length equal to 2, the Y length equal to 4, and the Z length equal to 1, the Y direction is given the most weight and the Z direction is given the least weight. Points that are 4 units away in the Y direction have the same weight as points that are 1 unit away in the Z direction.
The General setting lets you specify three ellipsoid axes that are non-orthogonal. Points in the direction of the longest axis are given the most weight; points in the direction of the shortest direction are given the least weight.
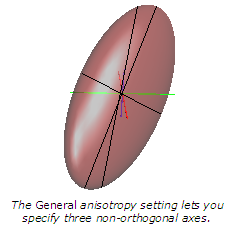
When using the General option, each axis in the ellipsoid is specified separately with a different vector. Sometimes axes of the ellipsoid will result in coplanar warnings. To understand how Voxler is calculating whether axes are coplanar, consider this diagram:
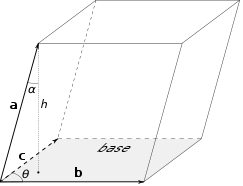
Vectors a, b, and c shown in 3D space.
Think of the vectors a, b, and c as being the positive rays of the three axes. These three axes are coplanar if the volume of the parallelepiped is zero. We know that the axes are not coplanar if the parallelepiped has non-zero volume. Sometimes, even when the rays create a volume that is greater than zero, round-off errors in the floating point numbers create a volume of zero. This can happen because the vectors a, b, and c that are specified are normalized into a unit cube where the longest of the lengths is 1.
See Also
How do I export a Gridder lattice to ASCII XYZC?