In Voxler, data are imported and connected to various modules to accomplish a useful task such as displaying scatter plots, isosurfaces, heightfields, and image slices. The type of data determines what type of module can be attached to it. Voxler supports several different data types. See the File Format Chart for a detailed list of supported file formats.
There are four main types of data: point sets, well data, lattices, and geometry. Each are discussed in detail below.
Point sets contain one or more three-dimensional point locations. Each location has an X, Y, and Z coordinate along with optional data components. A point can have any number of components. A component is a data variable associated with each point. Usually, this variable is the data you are trying to visualize, such as concentration.
Point data are collections of XYZ points in space, optionally with associated data values. Occasionally, this is called "XYZC data" where XYZ represent the three-dimensional position and C represents one or more data values at that position.
The WellData module is a container for well data imported into the project. Each well is imported into the Well Data module separately using the File | Import command. A Well Data module can have any number of wells, with each well containing information specific to that well. Each well can contain X, Y, Z, MD (Measured Depth), Azimuth, Inclination, and any number of Logs. The log is the data variable associated with the downhole location, and is usually the variable to be modeled.
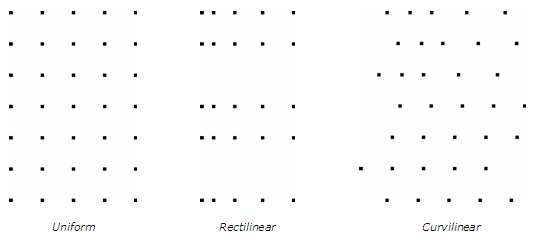
A lattice consists of a one-, two-, or three-dimensional data array. An array is a regular, structured matrix of points. A one-dimensional lattice is a line of data. A two-dimensional lattice is similar to an image or a Surfer grid. A three-dimensional lattice defines a three-dimensional volume. Each node (or point) in the lattice can contain one or more components or data values. Lattices are further categorized by the node geometry: uniform, rectilinear, and curvilinear. A single component lattice has a single data value (component) associated with each node. A multiple component lattice has two or more components per node.
Lattices can be further categorized by the geometry of the nodes:

The above diagrams are in two dimensions, but the actual lattice may be one-dimensional, two-dimensional, or three-dimensional.
Uniform |
Spacing between nodes is fixed in each direction, though the spacing in each of the three directions may be different. Uniform lattice axes are orthogonal. An image or bitmap is an example two-dimensional uniform lattice. Most medical data sets produced from an MRI or CT machine are three-dimensional uniform lattices.
|
|
Rectilinear |
Spacing is variable, but the axes are orthogonal (like log-log graph paper). The coordinates are explicitly stored for the lattice planes in the X, Y, and Z directions and must be monotonically increasing.
|
|
Curvilinear |
Spacing is variable, and the lattice axes are non-orthogonal. A curvilinear lattice has regular topology (like all lattices) but irregular geometry. The coordinates of each node are set independently. The lattice may be warped into any configuration in which the cells do not overlap (or self-intersect). Curvilinear lattices are often used in fluid dynamics. Since each node has its own set of three-dimensional coordinates, curvilinear lattices are the most general. They are also the most inefficient to work with, requiring more memory and time.
|
|
Lattices contain a data tuple at each node. A tuple consists of one or more data values (components). The number of components per tuple is fixed for any given lattice. Components are specified with a single primitive data type. These primitive types trade storage requirements for accuracy and range. The size specified in the table is the size to store a single value (in bytes).
Primitive Type |
Size |
Minimum |
Maximum |
Signed 8 bits |
1 |
-128 |
127 |
Unsigned 8 bits |
1 |
0 |
255 |
Signed 16 bits |
2 |
-32768 |
32767 |
Unsigned 16 bits |
2 |
0 |
65535 |
Signed 32 bits |
4 |
-2147483648 |
2147483647 |
Unsigned 32 bits |
4 |
0 |
4294967295 |
Signed 64 bits |
8 |
~ -9.223372e18 |
~ 9.223372e18 |
Float 32 bits |
4 |
~ -3.402823e+38 |
~ 3.402823e+38 |
Double 64 bits |
8 |
~ - 1.797693e+308 |
~ 1.797693e+308 |
· Unsigned 8-bit data is often called "byte" data.
· Lattice nodes are referenced by an index tuple ( i.j.k.), "i" being the index in the X direction, " j" being the index in the Y direction, and " k" being the index in the Z direction.
· Color data are stored within a lattice as RGBA byte values.
· The data are stored in a single memory block with the X direction varying fastest, followed by the Y direction, then followed by the Z direction. For example, assume a lattice with X, Y, Z dimensions of 2 x 3 x 2, two components per tuple, using BYTE primitives. The data block would have the following layout in memory, using the terminology (ZYXC):
|
0000, 0001, 0010, 0011, |
|
|
0100, 0101, 0110, 0111, |
|
|
0200, 0201, 0210, 0211, |
|
|
1000, 1001, 1010, 1011, |
|
|
1100, 1101, 1110, 1111, |
|
|
1200, 1201, 1210, 1211. |
|
The first byte is at the origin. The data block would be 24 bytes in size.
Geometry consists of triangles, texture maps, line segments, and other objects. Geometry is collected at the end of the network and displayed in the Viewer window. Geometry can be added from a data file, such as a DXF, SHP, BLN, or IV file, or can be created with a module, such as a Contours or Isosurface.
Blanking is fully supported in the point sets and lattices. Blanked data in Voxler is not represented by a special "flag" value. This allows the full range of a given primitive type to be used without being misrepresented as a blanked node. For example, if unsigned byte data were being stored in a lattice, values from 0 to 255 could be stored in the lattice without needing to reserve a special blanked value. This is all handled internally by Voxler.
Lattice nodes are commonly blanked in the Gridder module when the search criteria are not met; in Filter edge handling; and when a smaller input lattice is resampled to a larger output lattice (in which nodes outside the input lattice extents are blanked).
Blanked nodes are not displayed in output modules; however, they are written to exported data files if the export format supports them. For example, if a Surfer . GRD file is exported, the internal blank nodes within Voxler are converted to Surfer grid blank values in the output file.
See Also