 |
|Select the TestLattice module in the
Network Manager to display its properties
in the Property Manager.
The Network | Data Source | TestLattice command adds a TestLattice module to the Network Manager.
The TestLattice module generates a variety of predefined lattices that can be used for testing or experimenting with various modules. The output dimensions, limits, and primitive type may be specified for the output lattice.
The TestLattice has no input. To change the data displayed by the TestLattice, select the TestLattice module in the Network Manager and change the Function property in the Property Manager.
The TestLattice creates a uniform lattice. It may be connected to the Graphics Output Modules or the Computational Modules. An Info Module may also be connected to the output node.
Click on the TestLattice module in the Network Manager to select it. The TestLattice properties are displayed in the Property Manager. The available properties are described below.
 |
|
Select the TestLattice module in the
Network Manager to display its properties
in the Property Manager.
The FunctionLattice module contains the following tabs in the Property Manager:
General
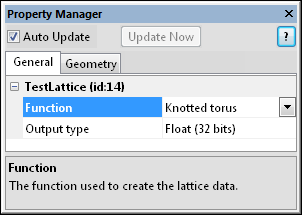
Test lattices are created using one of
six predefined Function options.
Choose the desired predefined Function to use to create the lattice data.
Examples of each of the function types appear below. References are located at the bottom of this page.
|
Knotted Torus |
The Knotted Torus function is based on equations presented by Poston, et al. |
|
|
Spherical Density |
The Spherical Density function models the distance squared from the point 0.5, 0.5, 0.5 over the unit cube ranging from 0.0 to 1.0. |
|
|
Vector Vortex |
The Vector Vortex function computes a spiral vector field. The x, y, and z components of the vector V at (x, y, z) are given by: · Vx = -y / s; Range = -1.0 to +1.0 · Vy = x / s; Range = -1.0 to +1.0 · Vz = α * z; Range = 0.0 to α
where s = sqrt(x*x + y*y), the radial distance in the xy plane. |
|
|
Wiffle Cube |
The Wiffle Cube function is a cube with a sphere removed from the center, as described by Bourke. |
|
|
Jack |
The Jack function simulates a jack (from the game of jacks) by creating a density function from four spheres and three ellipsoids. |
|
|
Knotted Rope |
The Knotted Rope function computes a distance function from the center of a knotted rope. Imagine a rope tied into a loose knot in which every point in the lattice is the minimum distance to the center of the rope. |
|
The Output Type is the numeric format used for the lattice X, Y, Z and component values stored in the output data. Select a Signed, Unsigned, Float, and Double output primitive type to be stored in the output lattice. The larger the output type, the larger the resulting lattice is. If you are using large coordinate or component values, you may need to use a larger output type, such as Float (32 bits) or Double (64 bits), but this will increase the output lattice size and the amount of memory needed to create the lattice. To change the type, click on the existing option and select the desired option from the list.
Bourke, P. (1990) Wiffle cube. Accessed at http:// astronomy.swin.edu.au/~ pbourke/surfaces/ wiffle.
Poston, T., Nguyen, H. T., Heng, P-A, and Wong, T-T. (1997) "Skeleton climbing": fast isosurfaces with fewer triangles. Proceedings of the 5th Pacific Conference on Computer Graphics and Applications. References can be accessed at http://www.cse.cuhk.edu.hk/~ttwong/papers/sc/sc.html
See Also